2.2 Calculations
2.2.1 Dimensioning a Roots pumping station
Various preliminary considerations are first required in dimensioning a Roots pumping station.Compression ratio
The compression ratio
Please update your browser. It looks like you are using an old version of the Microsoft Edge browser. To get the best experience with the Pfeiffer website, please update your browser.
Formula 2-1: Roots pump gas load
Formula 2-2: Compression ratio of Roots pump
Formula 2-3: Compression ratio of Roots pump for laminar flow
Formula 2-4: Compression ratio of Roots pump for molecular flow
Formula 2-5: Pumping speed of Roots pumping station with overflow valve open and at high fore-vacuum pressure
Physical Sign | Unit | Description |
|---|---|---|
Sv | [m3/h] | Pumping speed foreline pump at pressure pv |
p | [mbar] | Inlet pressure of roots pump |
[mbar] | Pressure difference adjusted at bypass valve | |
S | [m3/h] | Pumping speed at roots inlet flange |
Formula 2-6: Pumping speed of Roots pumping station with overflow valve closed and fore-vacuum pressure close to differential pressure
Formula 2-7: Pumping speed of Roots pumping station at high intake pressure
Formula 2-8: Pumping speed of Roots pumping station at low intake pressure
Formula 2-9: Pump-down time
Formula 2-10: Calculating the pumping speed
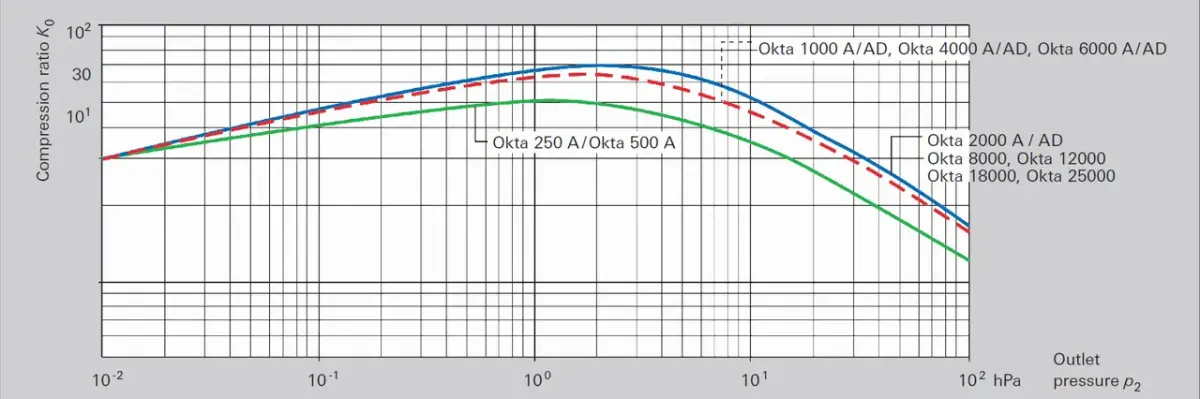
Figure 2.1: No-load compression ratio for air with Roots pumps

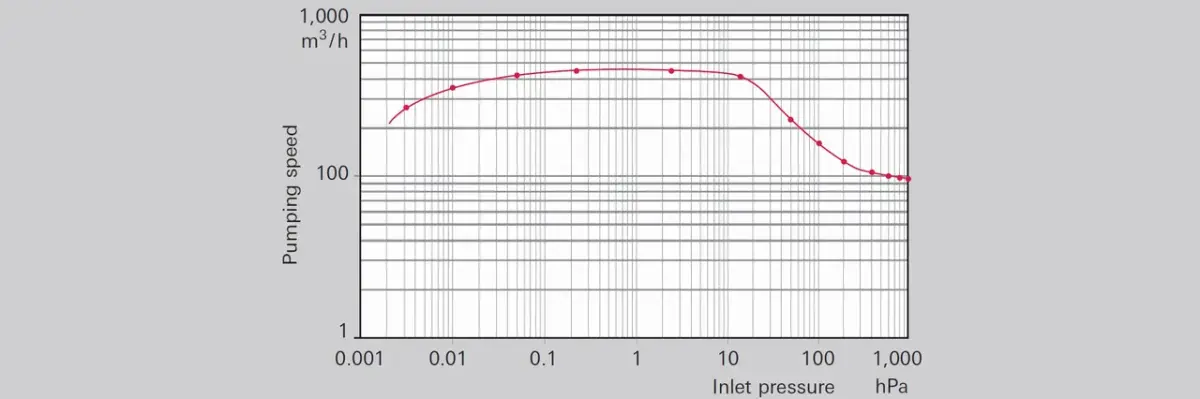
Figure 2.2: Volume flow rate (pumping speed) of a pumping station with Hepta 100 and Okta 500

Pa / hPa | Pv / hPa | Sv / (m3 / h) | Q / (hPa · m3/ h) | KΔ | K0 | S1 / (m3 / h) | S2 / (m3 / h) | t / h | t / s |
|---|---|---|---|---|---|---|---|---|---|
1,000.0000 | 1,053.00 | 90.00 | 94,770.00 | 1.05 | 94.77 | 0.00490 | 17.66 | ||
800.0000 | 853.00 | 92.00 | 78,476.00 | 1.07 | 98.10 | 0.00612 | 22.04 | ||
600.0000 | 653.00 | 96.00 | 62,688.00 | 1.09 | 104.48 | 0.00827 | 29.79 | ||
400.0000 | 453.00 | 100.00 | 45,300.00 | 1.13 | 113.25 | 0.01359 | 48.93 | ||
200.0000 | 253.00 | 104.00 | 26,312.00 | 1.27 | 131.56 | 0.00652 | 23.45 | ||
100.0000 | 153.00 | 105.00 | 16,065.00 | 1.53 | 7.00 | 160.65 | 321.56 | 0.00394 | 14.18 |
50.0000 | 103.00 | 105.00 | 10,815.00 | 2.06 | 13.00 | 216.30 | 382.20 | 0.00608 | 21.87 |
14.9841 | 56.00 | 110.00 | 6,160.00 | 18.70 | 18.00 | 2,053.33 | 411.10 | 0.00822 | 29.58 |
2.5595 | 10.00 | 115.00 | 1,150.00 | 36.00 | 449.30 | 0.01064 | 38.30 | ||
0.2300 | 1.00 | 105.00 | 105.00 | 50.00 | 456.52 | 0.00670 | 24.13 | ||
0.0514 | 0.30 | 75.00 | 22.50 | 46.00 | 437.39 | 0.00813 | 29.27 | ||
0.0099 | 0.10 | 37.00 | 3.70 | 40.00 | 375.17 | 0.00673 | 24.23 | ||
0.0033 | 0.06 | 15.00 | 0.90 | 39.00 | 270.42 | 0.00597 | 21.51 | ||
0.0018 | 0.05 | 5.00 | 0.25 | 37.00 | 135.29 | ||||
Pump-down time: 344.94 s | |||||||||
Table 2.1: Pumping speed of a Roots pumping station and pump-down times
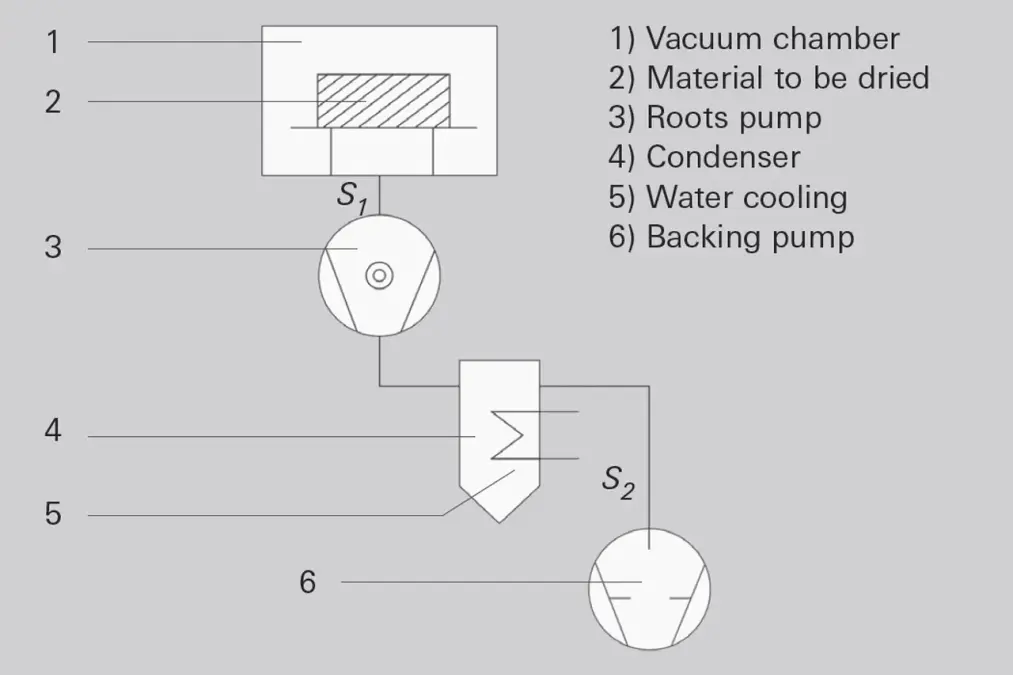
Figure 2.3: Drying system (schematic)

Formula 2-11: Gas throughput for pumping down vapors
T | Intake gas temperature | [K] |
R | General gas constant | [kJ kmol-1 K-1 |
t | time | [s] |
Pvc | Pressure in vacuum chamber | [Pa] |
mwater | [kg] | |
Mwater | Molar mass of water | [kg mol-1] |
mair | Air mass | [kg] |
Mair | Molar mass of air | [kg mol-1] |
T | Intake gas temperature | 300 K |
R | General gas constant | 8.314 kJ kmol-1 K-1 |
t | time | 3600 s |
Pvc | Pressure in vacuum chamber | 1000 Pa |
mwater | Water vapor mass | 10 kg |
Mwater | Molar mass of water | 0.018 kg mol-1 |
mair | Air mass | 0.5 kg |
Mair | Molar mass of air | 0.0288 kg mol-1 |
Formula 2-12: Calculation of the condensation surface area
Ak | Condensation surface area | [m2] |
Qwater | Specific enthalpy of evaporation | [Ws kg-1] |
mwater | Water vapor mass | [kg] |
ΔTm | Temperature differential between vapor and condensation surface | [K] |
k | Thermal transmission coefficient | [W m-2 K-1] |
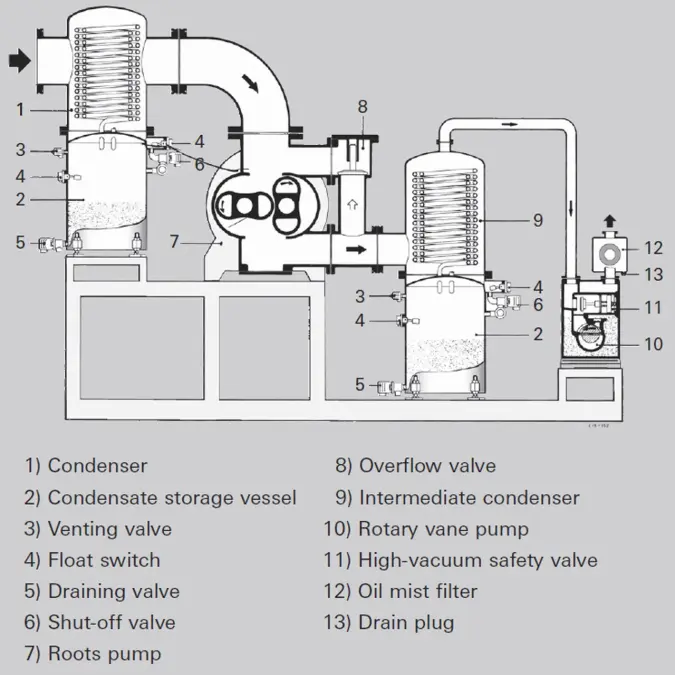
Figure 2.4: Roots pumping station for vapor condensation


Figure 2.5: Roots pumping station for vapor condensation

Figure 2.6: Roots pumping station for transformer drying


Formula 2-13: Base pressure of a vacuum system
pb | Base pressure | [Pa] |
Ql | Gas flow through leaks and permeation | [Pa m3 s-1] |
Qdes,M | Outgassing from the metal surface | [Pa m3 s-1] |
Qdes,K | Outgassing from the seals | [Pa m3 s-1] |
V | Vessel volume | 0.2 m3 |
A | Vessel surface | 1.88 m2 |
Ak | ealing surface of the FPM seal | 0.0204 m2 |
Ql | 1.0 ⋅ 10 -9Pa m3 s-1 | |
qdesM | Area-related desorption rate of stainless steel | 2.7 ⋅ 10 -4Pa m3 s-1 m-2 |
qdesK | Area-related desorption rate of FPM | 1.2 ⋅ 10 -4Pa m3 s-1 m-2 |
Formula 2-14: Diffusion coefficient (T)
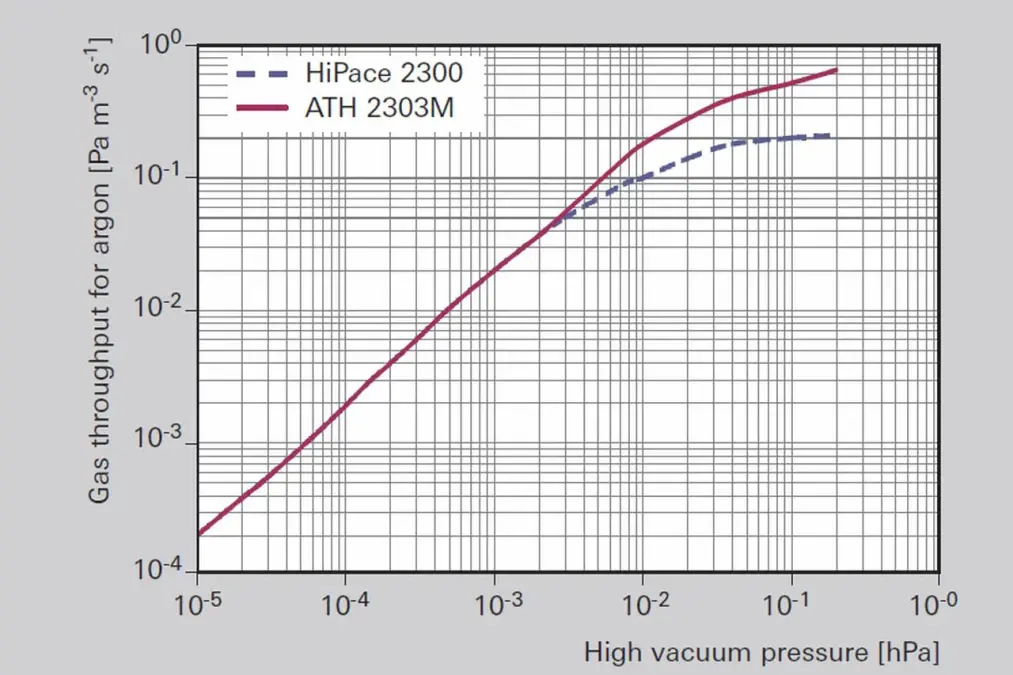
Figure 2.7: Gas throughput of different turbopumps at high process pressures

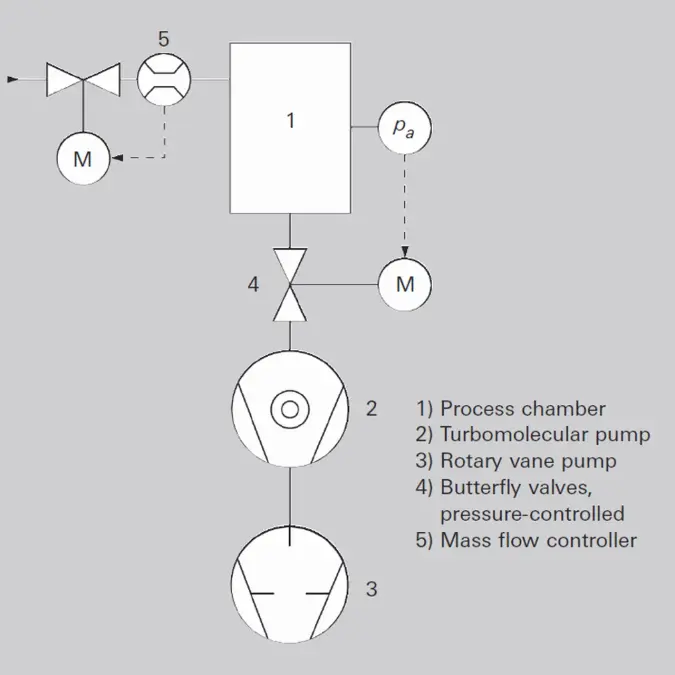
Figure 2.8: Vacuum system with pressure and throughput regulation
